Compression tables
6.1. Compression members: I and H sections
(a) Design resistance of the cross-section Nc,Rd
The design resistance is given by:
(i) For Class 1, 2 or 3 cross-sections:
Code ref
§6.2.4
§6.2.4 (2)
Nc,Rd = 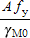
(ii) For Class 4 cross-sections:
N c,Rd = 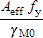
where:
| A | is the gross area of the cross-section |
| f y | is the yield strength |
| A eff | is the effective area of the cross-section in compression |
| γ M0 | is the partial factor for resistance of cross-sections ( γ M0 = 1.0, as given in the National Annex) |
For Class 1, 2 and 3 cross-sections the value of N c,Rd is the same as the plastic resistance, N pl,Rd given in the tables for axial force and bending, and is therefore not given in the compression tables.
For Class 4 sections the value of N c,Rd can be calculated using the effective areas tabulated in the effective section properties.
Rolled I and H sections which are Class 4 under axial compression alone according to EN 1993-1-1, are marked thus *.
The sections concerned are where the width to thickness ratios in Table 5.2 for parts subject to compression is:
Code ref
Table 5.2
c / t = d / t w > 42 ε for webs, and:
c / t = 0.5 ( b − t w − 2r ) / t f > 14 ε for flanges
where:
| d | is the depth of straight portion of the web (i.e. the depth between fillets) |
| t w | is the thickness of the web |
| t f | is the thickness of the flange |
| r | is the root radius |
| b | is the breadth of the section |
| ε | = ( 235 / f y )0.5 |
| ƒ y | is the yield strength |
(b) Design buckling resistance
Design buckling resistances for two modes of buckling are given in the tables:
Code ref
§6.3.1.1
- Flexural buckling resistance, about each of the two principal axes: N b,y,Rd and N b,z,Rd
- Torsional buckling resistance, N b,T,Rd
No resistances are given for torsional-flexural buckling because this mode of buckling does not occur in doubly symmetrical cross-sections.
(i) Design flexural buckling resistance, N b,y,Rd and N b,z,Rd
The design flexural buckling resistances N b,y,Rd and N b,z,Rd depend on the non-dimensional slenderness ( 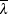 ), which in turn depends on:
), which in turn depends on:
- The buckling lengths ( L cr ) given at the head of the table
- The properties of the cross-section
The non-dimensional slenderness has been calculated as follows:
For Class 1, 2 or 3 cross-sections:
Code ref
§6.3.1.3
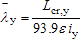 | for y-y axis buckling |
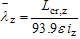 | for z-z axis buckling |
For Class 4 cross-sections:
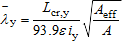 | for y-y axis buckling |
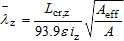 | for z-z axis buckling |
where:
| L cr,y , L cr,z | are the buckling lengths for the y-y and z-z axes respectively |
| i y , I z | are the radii of gyration about y-y and z-z axes respectively |
The tabulated buckling resistance is only based on Class 4 cross-section properties if this value of force is sufficient to make the cross-section Class 4 under combined axial force and bending. The value of n ( = N Ed / N pl,Rd ) at which the cross-section becomes Class 4 is shown in the tables for axial force and bending. Otherwise, the buckling resistance is based on Class 3 cross-section properties. Tabulated values based on the Class 4 cross-section properties are printed in italic type.
An example is given below:
533 x 210 x 101 UB S275
For this section, c / t = d / t w = 44.1 > 42 ε = 39.6
Hence, the cross-section is Class 4 under compression alone.
The value of axial force at which the section becomes Class 4 is N Ed = 2890 kN (see axial force and bending table, where n = 0.845 and N pl,Rd = 3420 kN ).
For L cr,y = 4 m N b,y,Rd = 3270 kN
The table shows 3270 kN in italic type because the value is greater than the value at which the cross-section becomes
Class 4
For L cr,y = 14 m N b,y,Rd = 2860 kN
The table shows 2860 kN in normal type because the value is less than the value at which cross-section becomes Class 4 (2890 kN).
(ii) Design flexural buckling resistance, N b,T,Rd
Code ref
§6.3.1.4
The design torsional buckling resistance N b,T,Rd depends on the non-dimensional slenderness ( 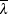 T ), which in turn depends on:
T ), which in turn depends on:
- The buckling lengths ( L cr ) given at the head of the table
- The properties of the cross-section.
The non-dimensional slenderness has been calculated as follows:
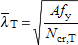 | for Class 1, 2 or 3 cross-sections |
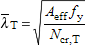 | for Class 4 cross-sections |
Code Ref.
Steelbiz document SN001[17]
where:
Code ref
Steelbiz document SN001[17]
| N cr,T | is the elastic torsional buckling force, given by 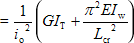 |
where:
| i 0 | 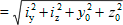 |
| y 0 and z 0 | are the coordinates of the shear centre with respect to the centroid. For a doubly symmetric cross-sections, the shear centre coincides with the centroid; then y0 = 0 and z0 = 0 |
6.3. Compression members: channels
(a) Design resistance of the cross-section N c,Rd
Code ref
§6.2.4
§6.2.4(2)
The design resistance is given by:
N c,Rd = 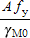
where:
| A | is the gross area of the cross-section |
| f y | is the yield strength |
| λ M0 | is the partial factor for resistance of cross-sections ( λ M0 = 1.0 , see National Annex) |
The value of N c,Rd is the same as the plastic resistance, N pl,Rd given in the tables for axial force and bending, and is therefore not given in the compression tables.
(b) Design buckling resistance
Design buckling resistance values are given for the following cases:
- Single channel subject to concentric axial force
- Single channel connected only through its web, by two or more bolts arranged symmetrically in a single row across the web
1. Single channel subject to concentric axial force
Design buckling resistances for two modes of buckling are given in the tables:
- Flexural buckling resistance about the two principal axes: N b,y,Rd and N b,z,Rd
- Torsional or torsional-flexural buckling resistance, whichever is less, N b,T,Rd
(i) Design flexural buckling resistance, N b,y,Rd and N b,z,Rd
Code ref
§6.3.1.3
The design flexural buckling resistances N b,y,Rd and N b,z,Rd depend on the non-dimensional slenderness ( 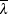 ), which in turn depends on:
), which in turn depends on:
- The buckling lengths (L cr) given at the head of the table.
- The properties of the cross-section.
- The non-dimensional slenderness, which has been calculated as follows:
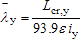 | for y-y axis buckling |
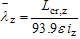 | for z-z axis buckling |
where:
| L cr,y , Lcr,z | are the buckling lengths for the y-y and z-z axes respectively. |
(ii) Design torsional and torsional-flexural buckling resistance, N b,T,Rd
Code ref
§6.3.1.4
The resistance tables give the minimum of the torsional and the torsional-flexural buckling resistance. These depend on the non-dimensional slenderness ( 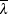 T ), which in turn depends on:
T ), which in turn depends on:
- The buckling lengths (L cr) given at the head of the table.
- The properties of the cross-section.
- The non-dimensional slenderness, which has been calculated as follows:
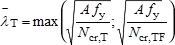
where:
| N cr,T | is the elastic torsional buckling force, 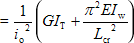 |
| i 0 |  |
| y 0 | is the distance along the y-y axis from the shear centre to the centroid of the gross cross-section. |
| N cr,TF | is the elastic torsional-flexural buckling force, = A σ TF |
| σ TF |  |
| σ Ey | 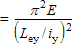 |
| σ T | = Ncr,T / A |
| β | = 1 − ( y 0 / i 0 )2 |
| L ey | the unrestrained length considering buckling about the y-y axis. |
2. Single channel connected only through its web, by two or more bolts arranged symmetrically in a single row across the web
Design buckling resistances for two modes of buckling are given in the tables:
Code ref
§6.3.1
- Flexural buckling resistance about the two principal axes: N b,y,Rd and N b,z,Rd
- Torsional or torsional-flexural buckling resistance, whichever is less, N b,T,Rd
(i) Design flexural buckling resistance, N b,y,Rd and N b,z,Rd
The design flexural buckling resistances N b,y,Rd and N b,z,Rd depend on the non-dimensional slenderness ( 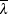 ), which in turn depends on:
), which in turn depends on:
- The system length (L) given at the head of the tables. L is the distance between intersections of the centroidal axes of the channel and the members to which it is connected.
- The properties of the cross-section.
- The non-dimensional slenderness, which has been calculated as follows:
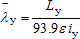 | for y-y axis buckling |
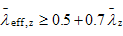 | for z-z axis buckling, where 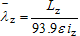 |
(Based on a similar rationale given in Annex BB.1.2 for angles)
Code ref
Annex BB.1.2
where:
| L cr,y , L cr,z | are the lengths between intersections |
| i y , I z | the radii of gyration about y-y and z-z axes |
| ε | = ( 235 / f y )0.5 |
(ii) Design torsional and torsional-flexural buckling resistance, N b,T,Rd
Code ref
§6.3.1.4
The torsional and torsional-flexural buckling resistance has been calculated as given above for single channels subject to concentric load.
6.4. Compression members: single angles
(a) Design buckling resistance:
Code ref
§6.3.1.1
Design buckling resistances for 2 modes of buckling, noted as F and T, are given in the tables:
- F: Flexural buckling resistance (taking torsional-flexural buckling effects into account), N b,y,Rd and N b,z,Rd
- T: Torsional buckling resistance, N T,Rd
(i) Design flexural buckling resistance, N b,y,Rd, N b,z,Rd
The tables give the lesser of the design flexural buckling resistance and the torsional flexural buckling resistance
The design flexural buckling resistances N b,y,Rd and N b,z,Rd depend on the non-dimensional slenderness ( 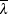 eff ), which in turn depends on:
eff ), which in turn depends on:
- The system length ( L cr ) given at the head of the tables. L is the distance between intersections of the centroidal axes (or setting out line of the bolts) of the angle and the members to which it is connected
- The properties of the cross-section
- The non-dimensional slenderness, which has been calculated as follows:
For two or more bolts in standard clearance holes in line along the angle at each end or an equivalent welded connection, the slenderness should be taken as:
For Class 1, 2 and 3 cross-sections:
Code ref
EN 1993-1-1 BB.1.2(2)
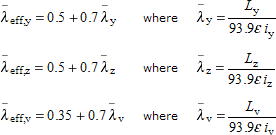 |
For Class 4 cross-sections:
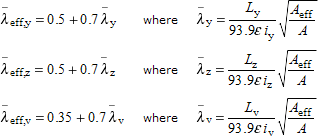 |
where:
| L y , L z and L v | are the system lengths between intersections. |
These expressions take account of the torsional flexural buckling effects as well as the flexural buckling effects.
In the case of a single bolt at each end, EN 1993-1-1 refers the user to §6.2.9 to take account of the eccentricity. (Note: no values are given for this case).
(ii) Design torsional buckling resistance, N b,T,Rd
Code ref
§6.3.1.3
The design torsional buckling resistance N b,T,Rd depends on the non-dimensional slenderness ( 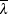 T ), which in turn depends on:
T ), which in turn depends on:
- The system lengths (L) given at the head of the table.
- The properties of the cross-section.
- The non-dimensional slenderness, which has been calculated as follows:
Code ref
§6.3.1.4(2)
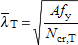 | for Class 1, 2 or 3 cross-sections |
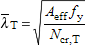 | for Class 4 cross-sections |
where:
| N cr,T | is the elastic torsional buckling force = 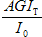 |
| G | 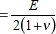 is the shear modulus is the shear modulus |
| E | is the modulus of elasticity |
| ν | is Poisson's ratio (= 0.3) |
| I T | is the torsional constant |
| I 0 | 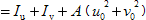 |
| I u | is the second moment of area about the u-u axis |
| I v | is the second moment of area about the v-v axis |
| u 0 | is the distance from shear centre to the v-v axis |
| v 0 | is the distance from shear centre to the u-u axis |