Tension tables
7.1. Tension members: Single angles
For angles in tension connected through one leg, EN 1993-1-1, §6.2.3(5) refers to EN 1993-1-8, §3.10.3. However this clause does not cover the case of more than one bolt in the direction perpendicular to the applied load. Therefore the resistance has been calculated using expressions from BS 5950-1 for angles bolted and welded through one leg. The resistance is independent of the number of bolts along the angle and their spacing. Tables only give values for the cross-sectional check; see AD351 [12] for more information.
Code ref
§6.2.3
§6.2.3 (2)
The value of the design resistance to tension N t,Rd has been calculated as follows:
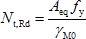
where:
| A eq | is the equivalent tension area of the angle |
| f y | is the yield strength |
| γ M0 | is the partial factor for resistance of cross-sections ( = 1.0, as given in the National Annex) |
The equivalent tension area of the section A eq is given by:
| For bolted sections: | A eq = A e − 0.5 a 2 |
| For welded sections: | A eq = A e − 0.3 a 2 |
where:
| A e | = a e1 + a e2 but A e ≤ 1.2 ( a n1 + a n2 ) |
| a e1 | = K e a n1 but a e1 ≤ a 1 |
| a e2 | = K e a n2 but a e2 ≤ a 2 |
| K e | = 1.1 for grade S355 |
| = 1.0 for grade S460 | |
| a n1 | = a 1 − n bolts − d 0 t |
| a 1 | = h × t if the long leg is connected |
| = b × t if the short leg is connected | |
| n bolts | is the number of bolts |
| d 0 | is the diameter of the hole |
| a n2 | = a 2 |
| a 2 | = A − a 1 |
| A | is the gross area of a single angle |
Note: A block tearing check (EN 1993-1-8, §3.10.2) is also required for tension members. However, block tearing resistances have not been tabulated, as there are too many variables in the possible bolt arrangements.